Generalized dose-escalation safety schematics via Complete Path Enumeration (CPE)

Aims

Norris (2020b) proposed a universal schematic for evaluating the safety of the 3+3 dose-escalation design, and conjectured that the dose transition pathways (DTP) of Yap et al. (2017) would enable a similar treatment of model-based designs. This vignette demonstrates the fulfillment of that promise, in a demonstration of complete path enumeration (CPE) implemented efficiently for the continual reassessment method (CRM).

Generalized exact simulation of dose escalation

Dose-escalation trial designs commonly operate with a fixed set of $D$ prespecified doses, enrolling participants in small cohorts each of size $n$, at doses selected sequentially according to observed counts of binary dose-limiting toxicities (DLTs). Under such designs, the observations at any point in the trial may be recorded in a $C \times D$ matrix of toxicity counts $\{0, 1, ..., n, -\}$, with ‘$-$’ being used where a cohort has not been enrolled. Indeed, for deterministic designs in which dose-escalation decisions depend strictly on the history of observed DLT counts, such matrices suffice to account for the full dose-escalation sequence.¹ For designs with upper bounds on enrollment, $C$ may be fixed ex ante, and all possible paths comprehensively enumerated.

In Norris (2020b), for example, paths through the 3+3 design could be represented as $2 \times D$ matrices because the 3+3 design enrolls at most 2 cohorts at any given dose. The mathematical treatment offered there for the path matrices $T_{c,d}^j$ was independent of the 3+3 rules, however, and carries forward generally:

Denoting the prespecified doses by $(X_d)$ and the cumulative distribution function of $\mathrm{MTD}_i$ by $P$, we can write the vector $(\pi^j)$ of path probabilities:²

\[ \begin{align} p_d &= P(\mathrm{MTD}_i< X_d)\quad\mbox{(dose-wise toxicity probabilities)}\\ q_d &= 1 - p_d\\ \pi^j &= \prod_{c,d} {n \choose T_{c,d}^j} p_d^{T_{c,d}^j} q_d^{(n-T_{c,d}^j)}\quad\mbox{(path probabilities)} (\#eq:pi) \end{align} \]

Again as in Norris (2020b), taking logs in @ref(eq:pi) we find:

\[ \log \boldsymbol{\pi} = \sum_{c,d} \log {n \choose T_{c,d}} + \sum_c [T_{c,d},n-T_{c,d}]\left[{ \log \mathbf{p} \atop \log \mathbf{q}} \right] = \mathbf{b} + \mathrm{U}\left[{ \log \mathbf{p} \atop \log \mathbf{q}} \right], (\#eq:log-pi) \] where the $J \times 2D$ matrix $U$ and the $J$-vector $\mathbf{b}$ are characteristic constants of the given dose-escalation design.

Finally, we may as previously introduce the log-therapeutic index $\kappa$, enabling us to write the fatal (grade-5) fraction $f_d$ of DLTs as:

\[ f_d = \frac{P(e^{2\kappa} \mathrm{MTD}_i< X_d)}{P(\mathrm{MTD}_i< X_d)}, (\#eq:fatal-fraction) \]

in terms of which the expected number of fatal toxicities is:

\[ \boldsymbol{\pi}^\intercal \mathrm{Y} \mathbf{f}, (\#eq:fatalities) \]

where $\mathrm{Y} = \sum_c T_{c,d}^j$ denotes the $(J \times D)$ left half of $\mathrm{U}$.

Connection with DTP

Dose transition pathways (DTP) seem to have been introduced primarily as a means to reconcile model-based formulations of dose-escalation trials with the habitually rule-based thinking of clinicians. Specifically, Yap et al. (2017) cites 3 specific “perceived challenges” in making the transition from rule-based to model-based designs:

The “flexibility” of model-based designs (which I take to mean the additional free parameters they introduce into the design space) creates choices which cannot readily be appreciated in the rule-based terms familiar to clinical investigators.
Benefits of model-based designs are likewise not apparent to clinical investigators, against the background of “rule-based designs perceived to be ‘successful’ for decades”.
From the trialist’s perspective, the ‘black-box’ recommendations of model-based designs “contrast unfavorably with the transparent, simple rules of a rule-based design.”

To meet these challenges, DTP effectively transforms a model-based design into a rule-based design locally — so that its immediate operation several steps ahead can be ‘eyeballed’ by trialists as a small set of (say, $4^4 = 64$) distinct paths. The exhaustive enumeration employed here as in Norris (2020b) differs conceptually in its global reach (reflected in the ‘CPE’ moniker), and in its intent to support computation over the paths as opposed to cursory inspection. Supporting this expansive concept has required significant programming effort; the implementation of CPE in package precautionary is hundreds of times faster than the DTP of package dtpcrm (Yap et al. 2019) on the VIOLA trial example below.

An application

We will adopt the same parameters as in the dtpcrm package vignette:³

VIOLA set-up

Clinical parameters

number.doses <- 7
start.dose.level <- 3
max.sample.size <- 21
target.DLT <- 0.2
cohort.size <- 3

Note that the sample size limit allows us to set $C=7$.

Model specification parameters

prior.DLT <- c(0.03, 0.07, 0.12, 0.20, 0.30, 0.40, 0.52)
prior.var <- 0.75

Early stopping

stop_func <- function(x) {
  y <- stop_for_excess_toxicity_empiric(x,
                                        tox_lim = target.DLT + 0.1,
                                        prob_cert = 0.72,
                                        dose = 1)
  if(y$stop){
    x <- y
  } else {
    x <- dtpcrm::stop_for_consensus_reached(x, req_at_mtd = 12)
  }
}

Complete Path Enumeration (CPE)

t0 <- proc.time()
crm <- Crm$new(skeleton = prior.DLT,
               scale = sqrt(prior.var),
               target = target.DLT)$
  stop_func(stop_func)$
  no_skip_esc(TRUE)$
  no_skip_deesc(FALSE)$
  global_coherent_esc(TRUE)


crm$trace_paths(
      root_dose = start.dose.level,
      cohort_sizes = rep(3, 7))

## Registered S3 method overwritten by 'dtpcrm':
##   method    from 
##   print.mtd dfcrm

proc.time() - t0 # ~3sec on a 2.6GHz Quad Core i7; was ~17min with dtpcrm v0.1.1

##    user  system elapsed 
##   1.763   0.091   1.059

This yields all elements of the matrix formalism laid out in equations @ref(eq:pi)–@ref(eq:fatalities) above:⁴

T <- crm$path_array()

## T (4693×7×7) constructed in 0.125 sec
## T condensed in 0.177 sec

dim(T)

## [1] 4693    4    7

Compute $\mathbf{b} = \sum_c {n \choose T_{c,d}}$

b <- apply(log(choose(3, T)), MARGIN = 1, FUN = sum, na.rm = TRUE)
length(b)

## [1] 4693

Compute $\mathrm{U}$ and $\mathrm{Y}$

Y <- apply(T, MARGIN = c(1,3), FUN = sum, na.rm = TRUE)
Z <- apply(3-T, MARGIN = c(1,3), FUN = sum, na.rm = TRUE)
U <- cbind(Y, Z)
dim(U)

## [1] 4693   14

Derive $\mathbf{\pi}$ from the CRM skeleton, to check that $\sum_j \pi^j \equiv 1$

log_p <- log(prior.DLT)
log_q <- log(1 - prior.DLT)
log_pi <- b + U %*% c(log_p, log_q)
sum(exp(log_pi)) # check probabilities sum to 1

## [1] 1

Comparison with the DTP formulation

With each of (up to) 7 cohorts having 4 possible outcomes (0, 1, 2 or 3 toxicities), the DTP tabulation of dtpcrm lists a total of $4^7 = 16384$ paths. These are not all distinct paths, however, since early stopping results in path degeneracy.⁵ For example, we can see that paths 1005–1008 all terminate at the 6th cohort, resulting in a $4\times$ degeneracy:

data(viola_dtp) # as originally generated by 'dtpcrm:calculate_dtps'
knitr::kable(viola_dtp[1000:1010,])

	D0	D1	D2	T3	D3	T4	D4	T5	D5	T6	D6	T7	D7
1000	3	4	5	3	3	3	1	2	1	1	1	3	NA
1001	3	4	5	3	3	3	1	2	1	2	1	0	1
1002	3	4	5	3	3	3	1	2	1	2	1	1	1
1003	3	4	5	3	3	3	1	2	1	2	1	2	NA
1004	3	4	5	3	3	3	1	2	1	2	1	3	NA
1005	3	4	5	3	3	3	1	2	1	3	NA	NA	NA
1006	3	4	5	3	3	3	1	2	1	3	NA	NA	NA
1007	3	4	5	3	3	3	1	2	1	3	NA	NA	NA
1008	3	4	5	3	3	3	1	2	1	3	NA	NA	NA
1009	3	4	5	3	3	3	1	3	1	0	1	0	1
1010	3	4	5	3	3	3	1	3	1	0	1	1	1

Paths terminating at the 5th cohort would be listed 16 times, and those terminating at the 4th cohort 64 times, etc. The net degeneracy indeed proves to be quite substantial, inflating the DTP table by a factor of 3.5:

viola_paths <- as.matrix(unique(viola_dtp))
dim(viola_paths)

## [1] 4693   15

To distinguish it from the degenerate DTP table returned by dtpcrm::calculate_dtps, we will refer to the unique listing as the path matrix. Note that in precautionary this is available straightaway from the Crm object crm after having invoked $trace_paths on it above:

pmx <- crm$path_matrix()
dim(pmx)

## [1] 4693   15

Fitting a lognormal $\mathrm{MTD}_i$ to VIOLA’s CRM skeleton

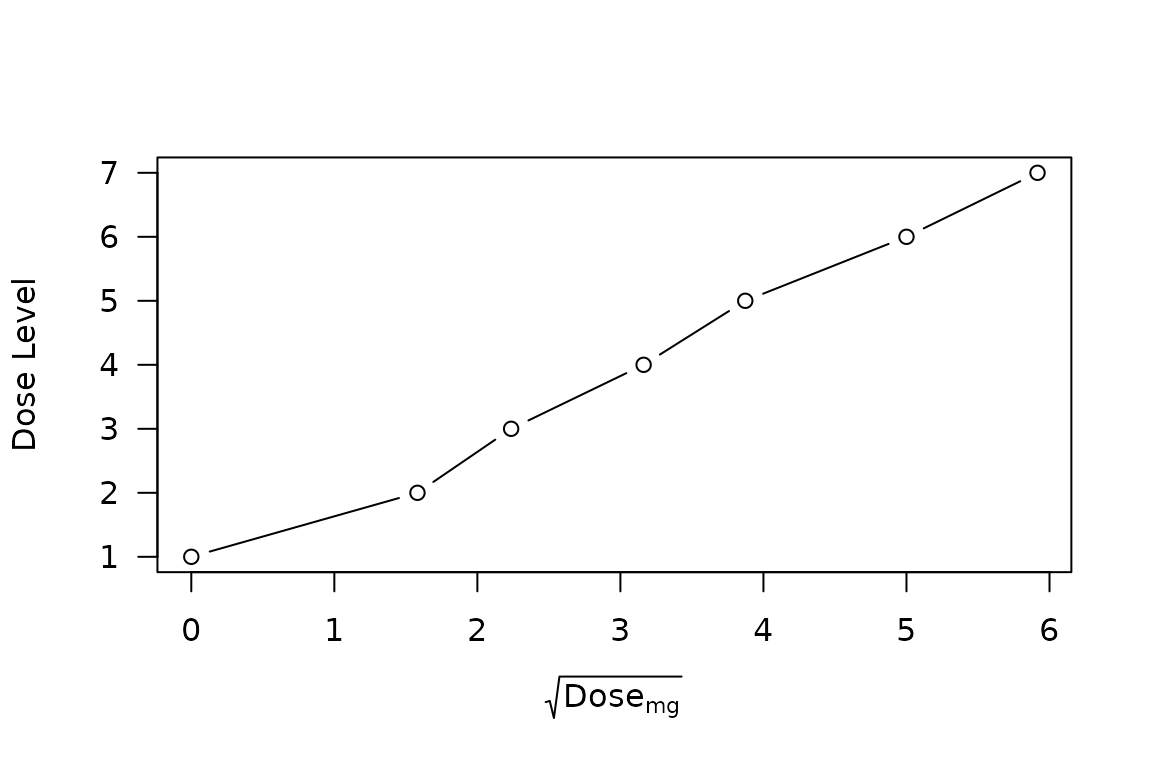
Whereas the analysis of Norris (2020b) was carried forth under a thoroughly logarithmic scaling of dose, the dosing intervals employed in the VIOLA trial are suggestive of an approximately square-root dose scaling—at least for the nonzero doses:

viola_dosing <-
  data.frame(Label = -2:4 # VIOLA dose designations -2,...,4
            ,Level =  1:7  # We use integer dose indexes here
            ,Dose_mg = c(0, 2.5, 5, 10, 15, 25, 35)
            ,skeleton = prior.DLT
             )
viola_dosing <- viola_dosing %>%
  mutate(log_dose = log(Dose_mg)
        ,sqrt_dose = sqrt(Dose_mg)
        )

plot(Level ~ sqrt_dose, data = viola_dosing, type = 'b'
     , ylab = "Dose Level"
     , xlab = expression(sqrt(Dose[mg]))
     , las = 1
     )

Indeed, the CRM skeleton looks quite close to a normal distribution under this scaling:

plot(skeleton ~ sqrt_dose, data = viola_dosing
     , type = 'b'
     , xlab = expression(sqrt(Dose[mg]))
     , ylim = c(0, 0.55)
     , las = 1)
x <- seq(0, 6, 0.1)
y <- pnorm(x, mean = sqrt(33), sd = 3)
lines(y ~ x, lty = 2)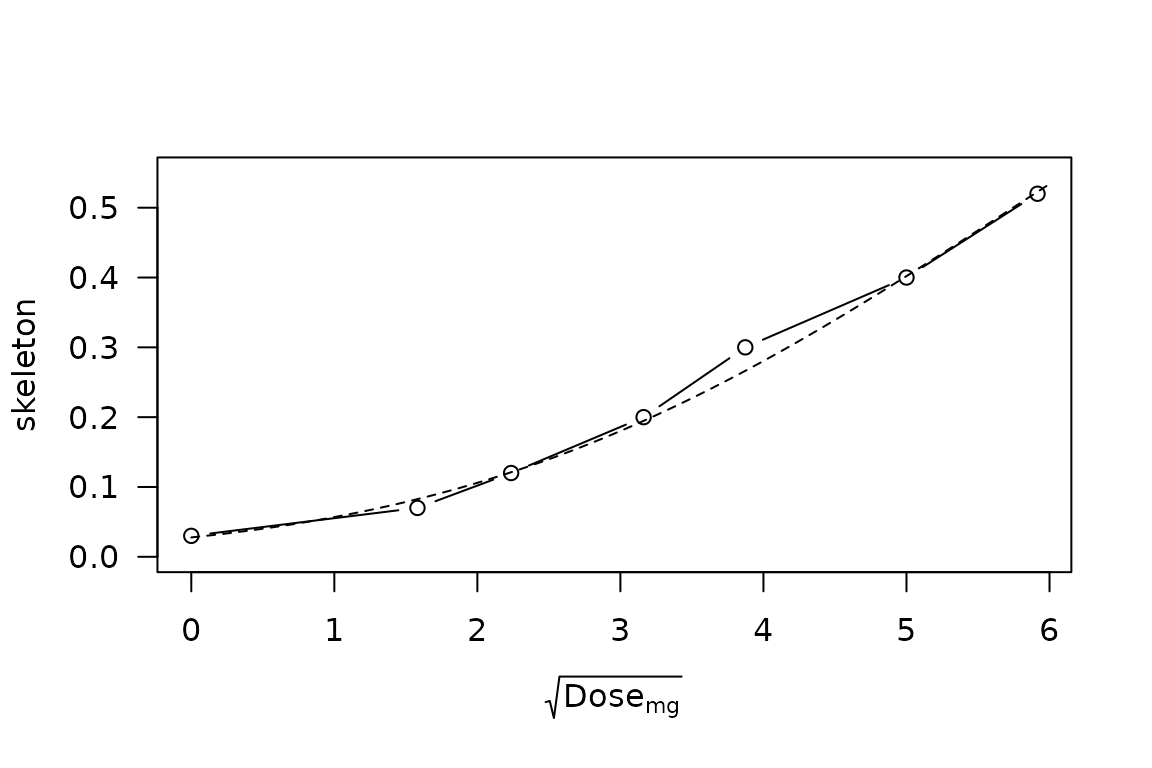

$CRM skeleton probabilities vs $\sqrt{\mathrm{Dose}}$, with superimposed normal distribution having median $\sqrt{33}$ and standard deviation 3.$

CRM skeleton probabilities vs $\sqrt{\mathrm{Dose}}$, with superimposed normal distribution having median $\sqrt{33}$ and standard deviation 3.

Nevertheless, the treatment of zero dose under this scaling is pharmacologically problematic, if not outright homeopathic, so we will proceed instead using a lognormal $\mathrm{MTD}_i$ distribution fitted to the CRM skeleton.

plot(skeleton ~ log_dose, data = subset(viola_dosing, is.finite(log_dose))
     , type = 'b'
     , xlab = expression(log(Dose[mg]))
     , xlim = c(0.5, 3.6)
     , ylim = c(0, 0.55)
     , las = 1)

sse <- function(mu_sigma, dose = viola_dosing$Dose_mg){
  mu <- mu_sigma[1]
  sigma <- mu_sigma[2]
  lnorm.DLT <- plnorm(dose, meanlog = mu, sdlog = sigma)
  sse <- sum((lnorm.DLT - prior.DLT)[dose > 0]^2)
}
fit <- optim(par = c(mu=log(38), sigma=1.8), fn = sse)
mu_opt <- log(round(exp(fit$par['mu']), 1))
sigma_opt <- round(fit$par['sigma'], 1)
x <- seq(0.5, 3.55, 0.05)
y <- plnorm(exp(x), meanlog = mu_opt, sdlog = sigma_opt)
lines(y ~ x, lty = 2)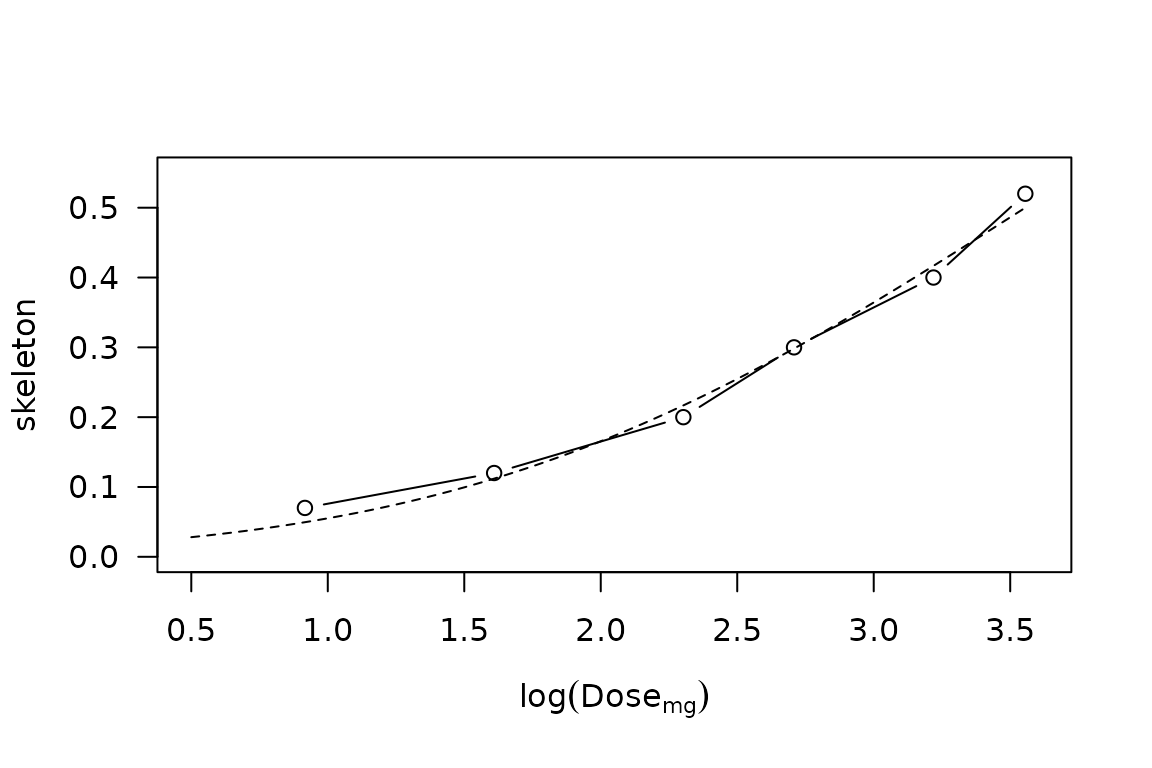

$CRM skeleton probabilities vs $\log \mathrm{Dose}$, with superimposed lognormal distribution having median $\mu = 35$mg and $\sigma = 1.6$.$

CRM skeleton probabilities vs $\log \mathrm{Dose}$, with superimposed lognormal distribution having median $\mu = 35$mg and $\sigma = 1.6$.

VIOLA safety

Taking this CRM skeleton fit as a modal expectation of the $\mathrm{MTD}_i$ distribution, we may employ Equations @ref(eq:fatal-fraction)–@ref(eq:fatalities) to obtain an expected number of fatal toxicities, as a function of $\kappa$:

f <- function(kappa, mu=mu_opt, sigma=sigma_opt, X=viola_dosing$Dose_mg) {
  # For ease of use, this function is VECTORIZED over kappa,
  # generally returning a length(X) x length(kappa) MATRIX
  # which can validly right-multiply Y in t(pi) %*% Y %*% f.
  # (In the special case length(kappa)==1, a vector is returned.)
  gr5 <- plnorm(outer(X, exp(-2*kappa)), meanlog = mu, sdlog = sigma)
  dlt <- plnorm(outer(X, exp( 0*kappa)), meanlog = mu, sdlog = sigma)
  ff <- gr5/dlt
  ff[is.nan(ff)] <- 0 # replace NaN caused by X[1]==0
  dimnames(ff) <- list(
    dose = paste0("X", seq_along(X)),
    kappa = round(kappa, 3)
  )
  if (length(kappa)==1)
    return(as.vector(ff))
  ff
}

kappa <- seq(0.2, 1.2, 0.02)
F <- f(kappa = kappa)
Ef <- t(exp(log_pi)) %*% Y %*% F
Ef <- t(Ef) # transpose to a column-vector
plot(Ef ~ kappa, type = 'l'
     , xlab = expression(kappa)
     , ylab = "Expected Number of Fatal DLTs"
     , las=1)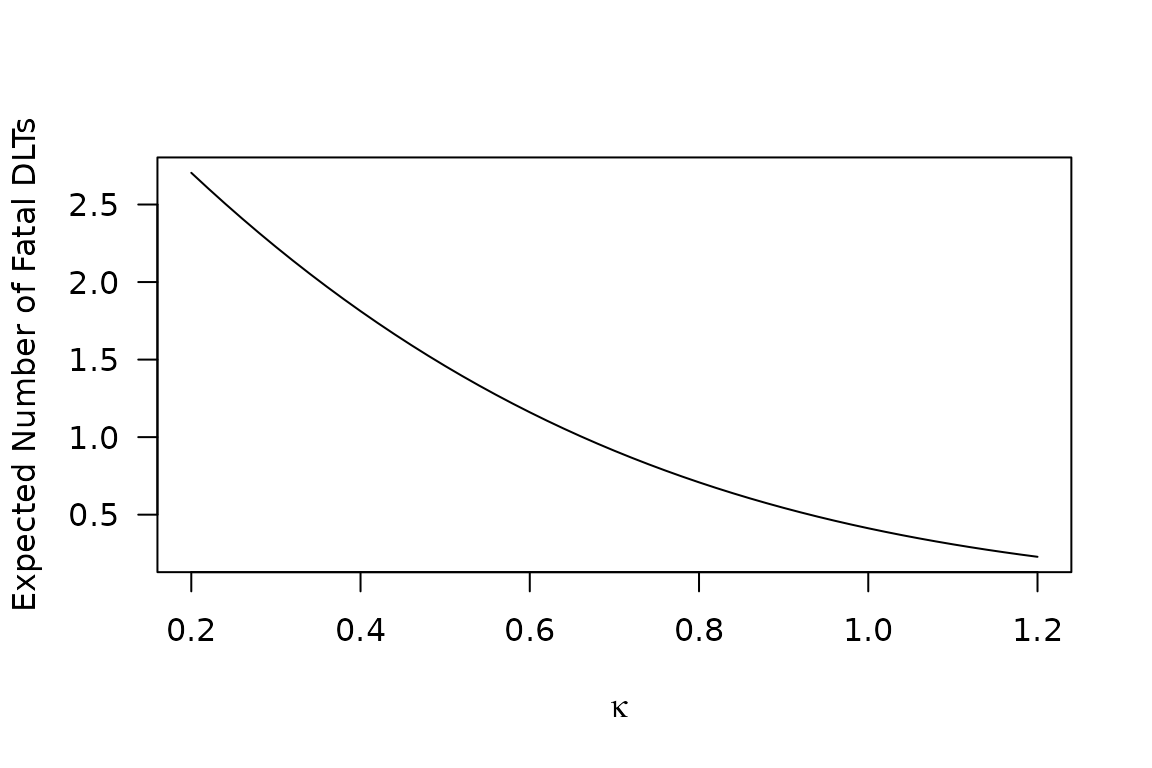

Beyond the skeleton

The development of CRM methods has left the status of the skeleton somewhat ambiguous. While evading its realistic interpretation as an $\mathrm{MTD}_i$ distribution,⁶ CRM proponents often fixate on the skeleton as a natural starting point for simulation studies. Braun (2020), for example, develops an approach which “hinges on the assumption that the true DLT probabilities examined are consistent with the selected skeleton.”

Nevertheless, it is incumbent on trial methodologists to examine the safety characteristics of their designs under conditions of model misspecification. The technique of Figure 3 in Norris (2020b) provides one approach.

To enable parameter departures from our lognormal skeleton fit, we require $\log \boldsymbol{\pi}$ as a function of $(\mu, \sigma)$:

log_pi <- function(mu, sigma){
  p <- plnorm(viola_dosing$Dose_mg, meanlog = mu, sdlog = sigma)
  log_pq <- c(log(p), log(1-p))
  log_pi = b + U %*% pmax(log_pq, -500) # clamping -Inf to -500 avoids NaN's  
}

This enables us to compute expected fatalities as a scalar field on a 3-dimensional space defined by parameters $(\mu, \sigma, \kappa)$. But again as in Norris (2020b) we employ a minimax framing of our safety question, to achieve a dimension reduction:

mu_minimax <- log(viola_dosing$Dose_mg)[3] # dose 3 is 2nd-highest *nonzero* dose

The irregularly spaced doses of VIOLA don’t yield a unique delta, but the $2\times$ multipliers either side of dose level 3 (our mu_minimax) allow us to select $\delta = \log 2$ as a local approximation:

delta <- mean(diff(log(viola_dosing$Dose_mg)[2:4]))

We may now generate a grid of values, and plot contours:

focustab <- CJ(mu = mu_minimax
              , K = seq(0.5, 1.65 , 0.01) # K = kappa / sigma
              , sigma = delta/seq(0.4, 2.2, 0.01)
              )
focustab[, kappa := K * sigma]
focustab[, value := t(exp(log_pi(mu,sigma))) %*%
             Y %*% f(kappa=kappa, mu=mu, sigma=sigma)
       , by = .(mu,sigma)]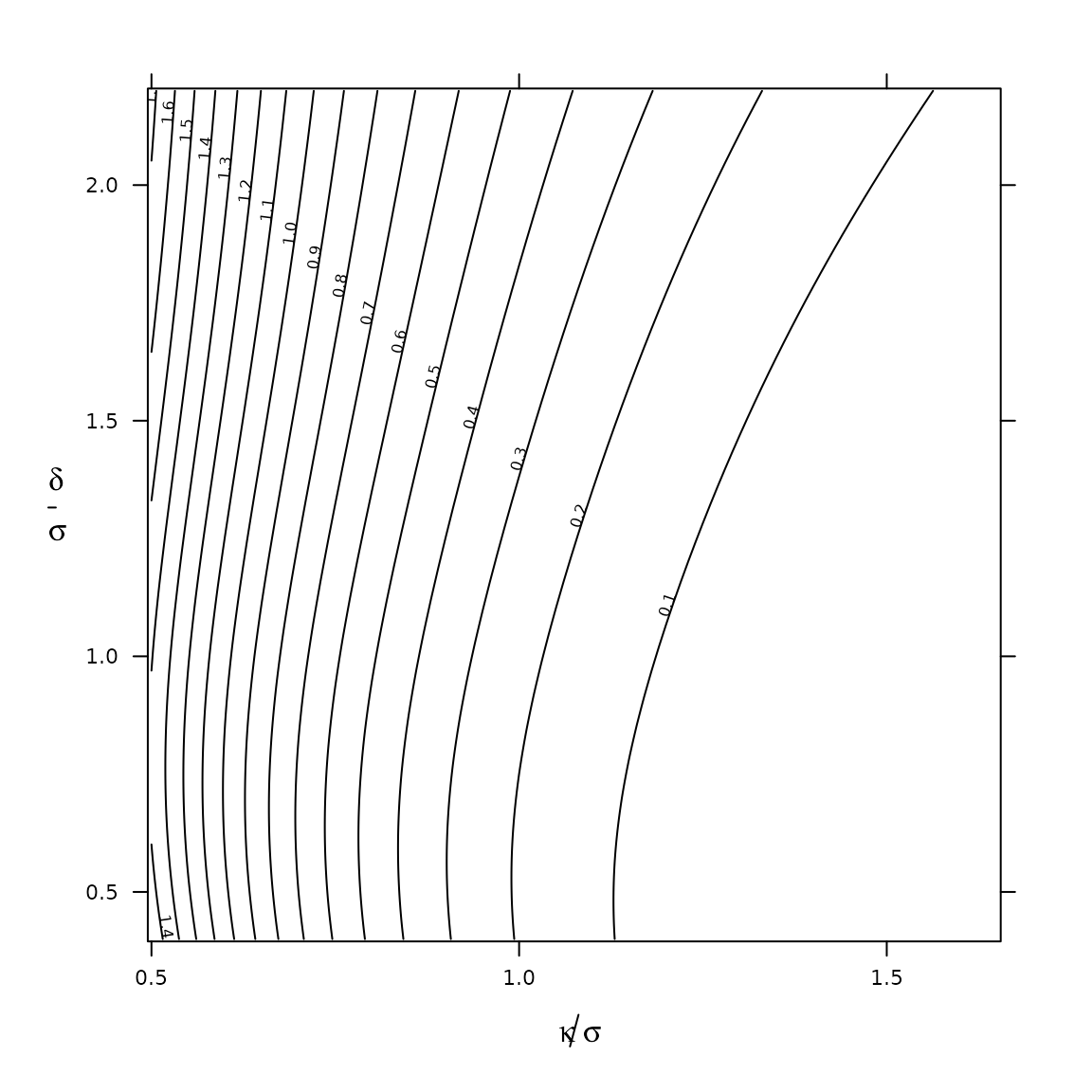

$Ex ante expectation of fatalities in the VIOLA trial, under the analytical set-up of Figure 3 in @norris_what_2020. Therapeutic index $\kappa/\sigma$ gauges the target drug's aptness for safe-and-effective 1-size-fits-all dosing in the trial's combination regimen. Signal-to-noise index $\delta/\sigma$ governs the informativeness of the dose-escalation process. This analysis assumes a log-normally distributed $\MTDi$, with median parameter set (on minimax grounds) at VIOLA dose level 3. Plotted values of $\delta/\sigma$ are based on $\delta=\log(2)$, selected according to the $2\times$ VIOLA dose-level spacing around this dose level.$

Ex ante expectation of fatalities in the VIOLA trial, under the analytical set-up of Figure 3 in Norris (2020b). Therapeutic index $\kappa/\sigma$ gauges the target drug’s aptness for safe-and-effective 1-size-fits-all dosing in the trial’s combination regimen. Signal-to-noise index $\delta/\sigma$ governs the informativeness of the dose-escalation process. This analysis assumes a log-normally distributed $\mathrm{MTD}_i$, with median parameter set (on minimax grounds) at VIOLA dose level 3. Plotted values of $\delta/\sigma$ are based on $\delta=\log(2)$, selected according to the $2\times$ VIOLA dose-level spacing around this dose level.

Conclusion

Although initially put forward with different intent, the dose transition pathways of Yap et al. (2017) render the enumerative approach of Norris (2020b) immediately applicable to the CRM. Importantly, the analysis is found to be computationally feasible in the setting of an actual trial. Indeed, with performance improvements debuted in version 0.2-2 of precautionary, the complete VIOLA enumeration becomes essentially trivial, taking just a few seconds on modern desktop hardware. This raises the prospect of scaling up our problems to meet the opportunities of massive parallelism (Gustafson 1988), expanding this mode of analysis to ever larger dose-finding trials.⁷

The approach taken here exemplifies a widely applicable scheme for the safety analysis of dose-escalation trials generally, rooted in the exhaustive enumeration of all possible trial paths.

References

Braun, Thomas M. 2020. “A Simulation‐free Approach to Assessing the Performance of the Continual Reassessment Method.” Statistics in Medicine, September, sim.8746. https://doi.org/10.1002/sim.8746.

Craddock, Charles, Daniel Slade, Carmela De Santo, Rachel Wheat, Paul Ferguson, Andrea Hodgkinson, Kristian Brock, et al. 2019. “Combination Lenalidomide and Azacitidine: A Novel Salvage Therapy in Patients Who Relapse After Allogeneic Stem-Cell Transplantation for Acute Myeloid Leukemia.” Journal of Clinical Oncology: Official Journal of the American Society of Clinical Oncology, January, JCO1800889. https://doi.org/10.1200/JCO.18.00889.

Gustafson, John L. 1988. “Reevaluating Amdahl’s Law.” Communications of the ACM 31: 532–33.

Norris, David C. 2020a. “Comment on Wages et Al, Coherence Principles in Interval-Based Dose Finding. Pharmaceutical Statistics 2019, Doi:10.1002/Pst.1974.” Pharmaceutical Statistics, March. https://doi.org/10.1002/pst.2016.

———. 2020b. “What Were They Thinking? Pharmacologic Priors Implicit in a Choice of 3+3 Dose-Escalation Design.” arXiv:2012.05301 [stat.ME], December. https://arxiv.org/abs/2012.05301.

Yap, Christina, Lucinda J. Billingham, Ying Kuen Cheung, Charlie Craddock, and John O’Quigley. 2017. “Dose Transition Pathways: The Missing Link Between Complex Dose-Finding Designs and Simple Decision-Making.” Clinical Cancer Research: An Official Journal of the American Association for Cancer Research 23 (24): 7440–7. https://doi.org/10.1158/1078-0432.CCR-17-0582.

Yap, Christina, Daniel Slade, Kristian Brock, and Yi Pan. 2019. Dtpcrm: Dose Transition Pathways for Continual Reassessment Method. https://CRAN.R-project.org/package=dtpcrm.

To see this, consider that one may ‘read’ such a matrix, starting from the (deterministic) starting dose, and applying the (deterministic) design rules at each step. That is, a deterministic design by definition imposes a unique sequence on the entries in such a matrix.↩︎
Products or sums over $c$ or pairs $(c,d)$ are understood to be taken over the non-empty cohorts thus indexed. In R, this convention is easily applied by using NA to represent ‘$-$’ , and performing aggregate operations with option na.rm=TRUE.↩︎
See Table 1 in Craddock et al. (2019).↩︎
Those interested in implementation details may examine the abstract R6 superclass Cpe from which class Crm is derived.↩︎
Indeed, the underlying calculations exhibit an even more remarkable degree of degeneracy, which is exploited through memoization implemented in R6 class Crm of precautionary.↩︎
For a related perspective on interpretational issues, see Norris (2020a).↩︎
See also https://en.wikipedia.org/wiki/Gustafson%27s_law.↩︎

David C. Norris

1/12/2021; revised 4/02/2021; revised again 6/14/2021